In Teil 9 geht es um einen Aimbot bzw. genauer gesagt eine Aimbot-Implementation. Die genaue Mathematik wird zwar nicht ausgelassen, aber nur angeschnitten.
Im Grunde genommen gibt es zwei Arten einen Aimbot zu schreiben:
- Man holt sich per GetTagPos() die Position des Kopfes, wandelt den Vector3 in Screenkoordinaten (Vector2) um und verwendet SetCursorPos() der WindowsAPI auf den Punkt an. Das entspricht einer “Mausbewegung” zum Gegner.
- Man verwendet etwas Vector-Mathematik und rechnet den Winkel von Pos1 (eigene Pos) zu Pos2 (Gegnerpos) aus. Nun addiert man diesen Differenzwinkel dem eigenen ViewAngle hinzu und schon aimed man auf das Ziel.
In diesem Artikel wird Methode 2 verwendet, da es einfach präziser und sauberer ist. Am Rand: Mein erster Versuch für einen MW2 Bot mit einem DirectX Overlay hat Methode 1 verwendet ![]()
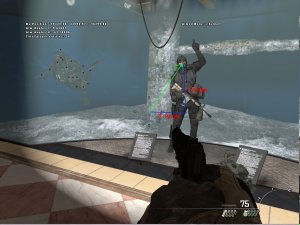
Nachdem meine tollen Paint-Skillz versagt haben muss nun ein Bild herhalten. Eigentlich wollte ich das ganze über ein 3D-Koordinatensystem illustrieren… Wie immer sollte man sich das Bild nicht nur verkleinert anschauen ![]()
Oben links sind Debugausgaben zu sehen, u.a. auch meine aktuellen ViewAngles. Dabei befindet sich die Y-Achse exakt gerade aus (parallel zum Boden) und der X-Wert zeigt nach “Norden”.
Im Aimbot laufen folgende Schritte in der VectorToViewangles ab, welche uns die Winkel zum Ziel liefert:
- Es wird ein neuer Vektor erzeugt, welcher von mir zum gezielten Punkt zeigt. (EnemyPos – MyPos).
- Es wird die Funktion VectorAngles aufgerufen, welche den übergebenen, soeben erzeugten Vektor, in Winkel relativ zum Koordinatenkreuz zurückliefert.
- Als nächstes wird die AnglesToAxis-Funktion aufgerufen. Sie erwartet die Winkel von der letzten Funktion sowie die 3 View-Angles der MW2-Kamera. (Up, Right, Forward). Dieser Winkel wird so also vom absoluten Koordinatensystem in das Koordinatensystem des Spielers umgewandelt.
- Nun wird von diesem Ergebniswinkel die aktuelle X und Y-Angles vom Spieler abgezogen und zurückgeliefert. Der weite Weg zur Differenz ist geschafft!
Wer sich noch etwas mehr mit der Mathematik beschäftigen möchte habe ich hier ein mehr oder weniger brauchbares Aimbot-Tutorial gefunden:
Das wars im auch schon, im Anschluss noch der Source. Credits gehen an das UC-Forum, dort geistert dieser Source rum. Ich habe ihn lediglich nach C# Portiert.
// ########################### Aim functions ################################## // Credits: UC-Forum public enum AimVars { PITCH = 0, YAW = 1, ROLL = 2, } public static Vector2 VectorToViewangles(Vector3 vAim) { Vector3 vecEntity; Vector3 vecAngle; vecEntity = vAim - GameManager.RefDef.Instance.vPos; vecAngle = VectorAngles(vecEntity); vecAngle.fX = -vecAngle.fX; if (vecAngle.fY > 180.0f) vecAngle.fY -= 360.0f; else if (vecAngle.fY < -180.0f) vecAngle.fY += 360.0f; if (vecAngle.fX > 180.0f) vecAngle.fX -= 360.0f; else if (vecAngle.fX < -180.0f) vecAngle.fX += 360.0f; AnglesToAxis(vecAngle, ref GameManager.RefDef.Instance.vView0, ref GameManager.RefDef.Instance.vView1, ref GameManager.RefDef.Instance.vView2); vecAngle.fY -= GameManager.RefDef.Instance.vAngles.fY; if (vecAngle.fY > 180.0f) vecAngle.fY -= 360.0f; else if (vecAngle.fY < -180.0f) vecAngle.fY += 360.0f; vecAngle.fX -= GameManager.RefDef.Instance.vAngles.fX; if (vecAngle.fX > 180.0f) vecAngle.fX -= 360.0f; else if (vecAngle.fX < -180.0f) vecAngle.fX -= 360.0f; return new Vector2(vecAngle.fY, vecAngle.fX); } static double radian(double degree) { double radian = 0; radian = degree * (3.1415926 / 180); return radian; } static void AngleVectors(Vector3 vAngles, Vector3 vForward, Vector3 vRight, Vector3 vUp) { float fAngle; float sr, sp, sy, cr, cp, cy; fAngle = (float)radian(vAngles.fX); sp = (float)Math.Sin(fAngle); cp = (float)Math.Cos(fAngle); fAngle = (float)radian(vAngles.fY); sy = (float)Math.Sin(fAngle); cy = (float)Math.Cos(fAngle); fAngle = (float)radian(vAngles.fZ); sr = (float)Math.Sin(fAngle); cr = (float)Math.Cos(fAngle); vForward.fX = cp * cy; vForward.fY = cp * sy; vForward.fZ = -sp; vRight.fX = (-1 * sr * sp * cy + -1 * cr * -sy); vRight.fY = (-1 * sr * sp * sy + -1 * cr * cy); vRight.fZ = -1 * sr * cp; vUp.fX = (cr * sp * cy + -sr * -sy); vUp.fY = (cr * sp * sy + -sr * cy); vUp.fZ = cr * cp; } static void AnglesToAxis(Vector3 vAngles, ref Vector3 vAxis0, ref Vector3 vAxis1, ref Vector3 vAxis2) { Vector3 vRight = new Vector3(0, 0, 0); AngleVectors(vAngles, vAxis0, vRight, vAxis2); vAxis1 = new Vector3(0, 0, 0) - vRight; //Marshal.StructureToPtr(GameManager.RefDef.Instance, new IntPtr(0x85EFB8), false); } public static Vector3 VectorAngles(Vector3 vForward) { float tmp; float yaw; float pitch; if (vForward.fY == 0 && vForward.fX == 0) { yaw = 0; if (vForward.fZ > 0) { pitch = 90; } else { pitch = 270; } } else { yaw = (float)(Math.Atan2(vForward.fY, vForward.fX) * 180 / 3.14159265); if (yaw < 0) { yaw += 360; } tmp = (float)Math.Sqrt(vForward.fX * vForward.fX + vForward.fY * vForward.fY); pitch = (float)(Math.Atan2(vForward.fZ, tmp) * 180 / 3.14159265); if (pitch < 0) { pitch += 360; } } return new Vector3(pitch, yaw, 0); } }